(ENEM PPL - 2019)No ano de 1751, o matemtico Euler
(ENEM PPL - 2019)
No ano de 1751, o matemático Euler conseguiu demonstrar a famosa relação para poliedros convexos que relaciona o número de suas faces (F), arestas (A) e vértices (V): V + F = A + 2. No entanto, na busca dessa demonstração, essa relação foi sendo testada em poliedros convexos e não convexos. Observou-se que alguns poliedros não convexos satisfaziam a relação e outros não. Um exemplo de poliedro não convexo é dado na figura. Todas as faces que não podem ser vistas diretamente são retangulares.
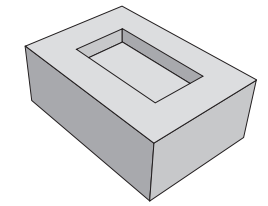
Qual a relação entre os vértices, as faces e as arestas do poliedro apresentado na figura?
A
V + f = A
B
V + f = A - 1
C
V + f = A + 1
D
V + f = A + 2
E
V + f = A + 3


